Mitsui's prime number theorem

I am being forced to read Mitsui's paper.

https://www.jstage.jst.go.jp/article/jjm1924/26/0/26_0_1/_pdf

Mitsui's prime number theorem

The main theorem of this paper says, in a simpified form, the following.

To state it, let $K$ be a number field and $\Vert - \Vert \colon O_K \to \mathbf R _{\ge 0}$ be the norm $\alpha \mapsto \max\limits _{ \iota \colon K\hookrightarrow \mathbf C} |\iota  (\alpha ) | $.

Theorem (Main Theorem on p. 35)

Let $\mathfrak a\subset O_K$ be a non-zero ideal and $b\in O_K$ an element coprime to $\mathfrak a$. For positive numbers $X$, denote by $\pi (\mathfrak a ,b ,X)$ the number of prime elements $\alpha \in O_K$ which are congruent to $b$ modulo $\mathfrak a$ such that $\Vert \alpha \Vert \le X $.

Then as $X\to +\infty $ we have 

\[ \pi (\mathfrak a ,b , X) = \frac{1 }{\varphi (\mathfrak a )\sqrt{|D_K|}\cdot  \mathrm{res} _{s=1} \zeta _K(s) }  \int _2^X \cdots \int _2^{X^2} \frac{\mathrm{d}t_1\cdots \mathrm dt_{r_1+r_2} }{\log (t_1\cdots t_{r_1+r_2} ) }  + O(X^n e^{-c \sqrt{n \log X} } ) ,  \] 

where we integrate $t_i$ up to $X$ if $1\le i\le r_1$ (the number of real embeddings) and up to $X^2$ if $r_1<i\le r_1+r_2$, and the constant $c>0$ depends only on the field $K$.

I suppose the value of the integral in the above formula is roughly equal to $X^n / (n\log X)$.

Structure of Mitsui's paper

Besides the unnumbered introduction, the paper consists of 4 sections.

In Section 1 (pp. 2-13), he proves the following asymptotic formula for the number of prime ideals of bounded norms (wasn't it known?): if $C \in Cl (K,\widetilde {\mathfrak a} )$ is a class in the ray class group with modulus $\widetilde{\mathfrak a} $, then as $x\to +\infty $, we have the estimate of the number of prime ideals belonging to $C$ in $Cl (K,\widetilde{\mathfrak a} ) $ and having norms $\le x$ :

\[ \pi (x,C )=\frac{1}{ | Cl (K, \widetilde{\mathfrak a} ) | } \int _2^x \frac{\mathrm d t}{\log t} + O(x e^{-c \sqrt{\log x} } ) .   \] 

In Section 2 (pp. 13-20), titled "Grössencharacter and preliminary lemmas," he spends 7 pages to do whatever preliminary that he needs later.

Section 3 spans through pp. 20-35 and is the technical heart. The main result of this section (p. 20) allows one to count the prime numbers in cone-shaped regions.

Section 4 consists of pp. 35-42. Here he deduces the main theorem above. He splits the cube $\{ \alpha \mid \Vert \alpha \Vert \le X \} $ into small quadrangular pyramids and applies the result of Section 3 to each of these pyramids.

I will discuss some details of Sections 3 and 4 below.

Section 3

I have to set up some notation to discuss the results of this section.

Recall that $r_1$ is the number of real embeddings $K\hookrightarrow \mathbf R $  and $r_2$ is the number of conjugate pairs of complex embeddings $K\hookrightarrow \mathbf C $. For the notational convenience, for an embedding $\iota \colon K\to \mathbf C $ let $| - | _\iota $  be the absolute value of $\iota (\alpha ) $ if $\iota $ is a real embedding, and $|\alpha |_\iota := |\iota (\alpha ) |^2$ if $\iota $ is complex.

Consider the multiplicative Minkowski map 

\[ O_K \setminus \{ 0\} \to \mathbf R ^{r_1+r_2} \]

defined by $\alpha \mapsto (\log | \alpha  |_\iota  )_{\iota \colon K\to \mathbf C}$.

Dirichlet's theorem says that the image of $O_K ^*$ is a lattice in the hyperplane $H= \{ (x_1,\dots ,x_{r_1+r_2}  ) \mid x_1+\dots +x_{r_1+r_2}=0 \} \subset \mathbf R^{r_1+r_2} $.

Then Theorem on p. 20 and Corollary on p. 35 says the following:

The number of prime elements having norms $\le x$ and lying in the depicted region is proportional to the area of the chosen region on the hyperplane $H$.

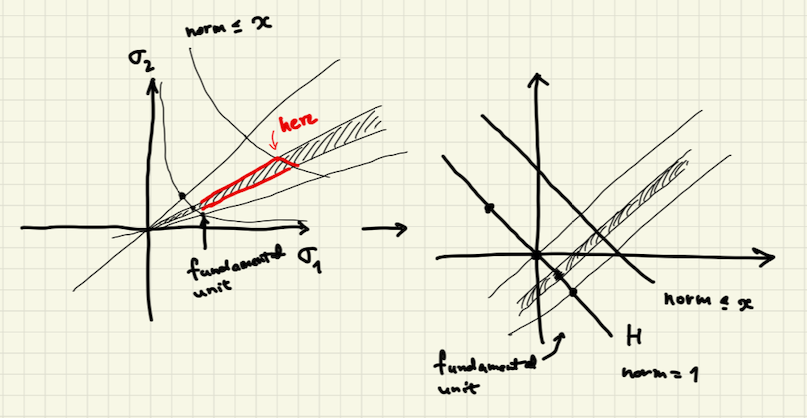
(If the chosen region is a fundamental paralellopiped, then the estimate is euqual to that in Theorem in Section 1.)

I guess now my task is to pin down exactly how and where analysis turns into the estimate of the number of prime elements. See you!

Section 4

Let me explain how he splits up the region $\Vert - \Vert \le X$.